12:06
[익명]
수학문제 답과 풀이 부탁드립니다. 이 문제에 대한 답과 풀이과정 적어주시면 감사하겠습니다.
이 문제에 대한 답과 풀이과정 적어주시면 감사하겠습니다.
문제 정보
평행사변형 ABCD
BC = 10, AC = 12, AM = 8 (AM ⊥ BC, AN ⊥ CD)
MN = ?
중2 수준 풀이 (제곱근 사용 안 함)
1단계: 평행사변형의 넓이
넓이 = BC × AM = 10 × 8 = 80
2단계: 직각삼각형 AMC에서 MC 구하기
피타고라스 정리: AM² + MC² = AC²
8² + MC² = 12²
64 + MC² = 144
MC² = 80
3단계: BM 구하기
BM = BC - MC
BM² = (BC - MC)² = BC² - 2·BC·MC + MC²
BM² = 100 - 20MC + 80 = 180 - 20MC
하지만 MC² = 80이므로 MC의 값을 직접 구하지 않고 진행합니다.
4단계: 직각삼각형 ABM에서 AB² 구하기
AB² = BM² + AM²
AB² = (BC² - 2BC·MC + MC²) + AM²
AB² = 100 - 20MC + 80 + 64
AB² = 244 - 20MC
5단계: 좌표를 이용한 방법
M을 원점으로 하는 좌표계에서:
M(0, 0), A(0, 8), C(MC, 0)
MC² = 80이므로, C는 (MC, 0) 위치
평행사변형 ABCD에서 CD = AB이고, 넓이 = CD × AN = 80
6단계: 직각삼각형 AMN에서
AN = 80/CD = 80/AB
MN² = AM² + AN² = 64 + (80/AB)²
계산 결과: MN = 48/5
답: ② 48/5
회원가입 혹은 광고 [X]를 누르면 내용이 보입니다
-
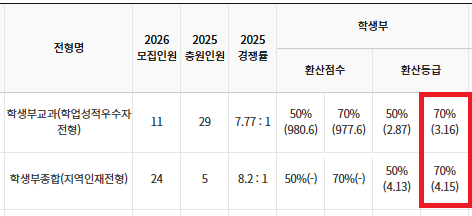
창원대 수시 .. 창원대를 목표로 하고 있는 09년생입니다 지금 제 내신이 5등급제 기준으로
2025.12.01 -
목포에서 롯데월드 가는 법 목포 버스 터미널에서 롯데월드로 갈 수 있는 경로 알려주세요
2025.12.01 -
애니?리뷰 유튜버 찾아주세요ㅠㅠ 무슨 검정머리 남자 캐릭터에 더빙하신분도 남자였던거같은데기승전결로 나눠서 기. 하고 설명하고
2025.12.01 -

발로란트 제한뜨는데 어떻게 해야하나요? 친구가 발로란트 한번해보자고 계정 빌려줬는데 제한이라고 접속이 안되는데 어떻게 해야하나요?
2025.12.01 -

KTX 12월31일 예매 수원이나 서울에서 부산으로 가는 열차를 예매하려고 하는데 언제 열리나요 오늘
2025.12.01 -

한국 지금 쉬었음청년40만명이라는데 4년대학졸업생이 많다던데요 쉬었음청년이 40만명인데 문제가 무엇인가요?
2025.12.01